誉田進学塾高校部日記

こんばんは。
八千代緑が丘校の轟です。

高校２年生のＡさんから、
数学の質問を頂きました。

このような問題でした。

図示すると、下図の点Ａ’の座標を求める
ことになります。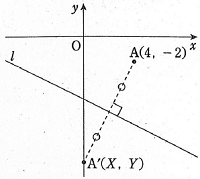

よくある解法としては、以下の２点を
数式に表して解くやり方があります。

Ａさんは、別の解法で解こうとしたけれど、
途中でつまづき、自分の考えのどこが
違っているのかを知りたいという質問でした。

Ａさんのように、学習している中で、
問題を解いてみたら掲載されている解説・解答とは
解法が違ったということは多くありますし、
ただ、自分の解き方のどこに誤りがあるのかを
自分ではわからないということもよくあります。

「とりあえず、このように解けばいいのか」
で終わらせずに、目の前の問題にトコトン対峙
するＡさんのような姿勢は素晴らしいと思います。

結果的に、Ａさんの考えていること自体は間違っては
いなかったのですが、ただし、解を得るためには、
そこに別の考え方を足し算する必要がありました。

この問題は、他にも解を得るために色々な解き方が
あります。

私でしたら、ベクトルを活用して解くか、
幾何学的に解くのが面白いかなと思います。

ベクトルを活用する場合、以下のように
解けます。

また、幾何学的に解くと以下のように
なります。

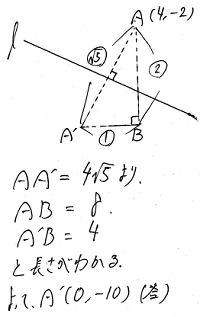
図形的にイメージしやすく、かつ
割と簡単な計算で解けると思います。

Ａさんには、このような別解もあるよと
解説をさせて頂きました。

今の時期の受験生にとっては、一つの問題を
じっくり考えるよりも、沢山の問題に触れたいと
思うと思いますし、正しい考え方だと思います。

ただ、寄り道と言いますか、思考力を磨くためには
「他にもどのような解き方があるだろうか」と
別解を思考錯誤しながら考えることも良い学びになります。
特に現在、高校１年生、２年生の方には、別解も意識
しながら学習に取り組んでいって頂けたらいいなと思います。

私は高校生の頃、長岡亮介先生(注1)の数学の授業を好んで
受けていたのですが、ある時、授業の中で長岡先生が
このようなことをおっしゃいました。
「最近の若者は、別解を考えることをしない。
　一昔前は、数学の問題を解く際、別解を考えることを
　楽しんでいたのに…」
と嘆いておられました。

高校生心に、長岡先生がそのようにおっしゃるのだから、
別解を考えることはとても重要なのだなと感じたことを
今でも鮮明に覚えています。
(数学の学習の取り組み方については、私は長岡先生から
多くの影響を受けたなぁと思います。)

実際の入試においても、普段から色々な視点で問題を解く
ことに慣れておくと、突破口を見出しやすいことは間違い
ありません。

思考力をつけることと、入試で合格の確度を上げることには
矛盾がないと思いますので、時には別解も考えながら、
数学とお付き合い頂ければ幸いです。

注1
　長岡亮介先生は高校生向けの学習参考書も多数手がけており、
　上智大学 理工学部 非常勤講師や明治大学 理工学部 数学科特任教授
　を務めてらっしゃった数学の先生。
　東進数学科の長岡恭史先生の実の兄。
　学生の頃は小田和正と一緒にバンド活動を行っていました。

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
10/27全国統一中学生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentochu/

11/4全国統一高校生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentoko/

一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE

★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんばんは。
八千代緑が丘校の轟です。

本日、武蔵野大学のＨＰにて
武蔵野大学の
『2025年度入試のムサシノスカラシップ選抜』
の入試情報について案内がリリースされました。

受験生の中には、年内に合格したいという方も
多いと思います。

また、最大４～６年間の授業全額免除
となるチャンスもあるため、
早い時期に入試にチャレンジしたい
という方には受験を検討する価値が
あるかと思います。

動画での案内はこちら↓
https://musashino-u.tv/admission-ch/2336/

入学試験要項のダウンロードはこちら↓
https://www.musashino-u.ac.jp/admission/download/faculty.html

ご興味のある方は、見てみてください。

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
10/27全国統一中学生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentochu/

11/4全国統一高校生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentoko/

一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE

★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは。
八千代緑が丘校の轟です。

最近、法政大学の英語について
ブログを書いてきました。

結局のところ、日頃から難易度の
高い英文を読んでいくことが良い対策になる
と、私なりの結論になったため、
ダメ押しで、再度、法政大学の英語について
書かせて頂きたいと思います。

長文自体は2022年やとか2021年など、
最新の英文が出題されていているため、
日頃から、新しい英文を読むように
意識することが大切です。

長文問題の中で、英文法の知識も
問われます。
純粋な読解問題だけというわけでは
ありません。

ですから、英文法の知識と、精読する力が
求められます。

また、過去問を解いていくと、
段々と、問題の難易度が上がってきているように
感じます。

法政大学の英語の難易度はＭＡＲＣＨの中でも
難しい方に入ってきているという印象を感じています。

近年の受験生たちの声を聞いていると、実際に
『法政大学の英語は想像していたよりも
　ずっと難しい！』
という声を聞きます。

英文自体の難易度は高いですが、
ただ、設問を解くという観点で言えば、
英文をしっかりと解釈できれば解けるように
設問は作られています。

ですから、法政大学の英語の攻略は、
難易度の高い英文をいかに読めるようになるか
ということですね。

取り組む問題集の難易度としては、
『関正生のThe Rules 英語長文問題集3 入試難関』
が丁度良いと思います。

著者　：関正生
出版社：旺文社

また、他にも英語長文であれば
『関正生の英語長文ポラリス[2 応用レベル]』
に取り組んで頂ければと思います。

著者　：関正生
出版社：KADOKAWA

そして、英文法の問題も出題されるため、
英文法の学習にも取り組んで頂きたいと思います。
そこで、お薦めの問題集は
『関正生の英文法ポラリス[2 応用レベル]』

著者　：関正生
出版社：KADOKAWA

法政大学の英語に関しては、
必要な学習を、必要な時間をかけて取り組めば、
必ず攻略することができると思います。

ですから、「これをしっかりと取り組むんだ！」
と決めて、やりきってください！

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
10/27全国統一中学生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentochu/

11/4全国統一高校生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentoko/

一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE

★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは。
八千代緑が丘校の轟です。

今回は、何が何でも法政大学 法学部に合格したい
という受験生に向けて、法政大学 法学部の
難易度、倍率、傾向、対策法を徹底解説していこうと思います。

「法政大学 法学部に合格したいけど、
　何から始めたらよいか分からない…」という受験生には
是非読んで頂きたいと思います。

【法政大学 法学部の概要】
法政大学の法学部は３つの学科で構成されています。
『法律学科』は法曹コースがあり、
現代社会の複雑多岐にわたる法的状況への対応力を育みます。

『政治学科』はあらゆる領域の問題を、
臨機応変に解決・処理できる能力を養います。

『国際政治学科』は観察力・分析力・構想力・交渉力
・実行力・そして英語を磨きます。

【入試概要】
受験方式は
①T日程（統一日程）
②英語外部試験利用
③A方式（個別試験）
④大学入学共通テスト利用
の4種類があります。

今回は①T日程　②英語外部試験利用　③A方式について
詳しくお話ししていきます。

＜T日程について＞
T日程の受験科目は以下のとおりです。

・国語または「数学I・Ⅱ、数学A・B」の2科目から1科目　（100点）
・英語　（150点）

※国語は古文・漢文の独立問題は出題しない
※数学Bは数列・ベクトルを出題範囲とする

T日程方式は学部併用が可能なので、
他の学部も気になっている、とにかく法政大学に合格したい
という方におすすめできます！
英語外部試験利用入試と併願もできます！

＜英語外部試験利用について＞
英語外部試験利用の受験科目は以下のとおりです

・国語または「数学I・Ⅱ、数学A・B」の2科目から1科目　（100点）

※国語は古文・漢文の独立問題は出題しない
※数学Bは数列・ベクトルを出題範囲とする

＜A方式について＞
A方式の受験科目は以下のとおりです。

・英語　（150点）　　国際政治学部のみ（200点）
・国語　（100点）
・「数学I・Ⅱ、数学A・B」「世界史探求」「日本史探求」
　「地理探求」「公民（政治経済）」の５科目から1科目　（100点）

一般入試の中で募集人数が最も多いため、学科がもう決まっている方、
学びたいことが明確な方はこちらを受験するのがおすすめです！

【科目別対策法　～英語編～】
まずは英語についてご紹介します。
法政大学法学部の英語は大問4問構成です。

大問4題とも長文読解問題で、問題数は40問。
試験時間は90分です。

長文読解問題は、どの大問も本文量が600語以上で、速読力が必要です。
主に空欄補充問題と語句整序問題で、
語彙力や熟語の知識、空欄箇所前後の内容把握、
文法力が問われます。

総合的な英語力が必要なため、早い段階からの対策が重要です。
日ごろから単語帳や熟語帳などを覚え、
問題演習を繰り返し、過去問演習で出題形式に慣れましょう。

全体的に見てみると、正誤問題が多く出題されています。
また、下線部の単語と同じ意味を持つ単語を聞かれる問題も多く見られました。

長文をなんとなくで読み進めてしまうと解けない問題がほとんどです。
長文は一文一文の集まりですから、まずは一文を正確に読めるようにしましょう。

そのためには英文解釈の力が必要不可欠です。
長文が読めるようになりたいけど何からやったらいいかわからない...
という方は『関正生の英文解釈ポラリス[1 標準~応用レベル] 』が
法政大学の英語対策におすすめです！

著者　：関 正生
出版社：KADOKAWA

【科目別対策法　～国語編～】
法政大学法学部の一般選抜の国語は、
大問3題で構成され、マーク式と記述式併用です。

大問1：現代文　評論（内容説明・空欄補充・内容一致など）
大問2：現代文　評論（空欄補充・内容説明・漢字問題など）
大問3：古文（内容説明・意味問題・文法・内容一致など）

試験時間は60分で、大問2題は現代文、1題は古文の構成です。
各大問で記述式問題が出題されます。

現代文は大問2題とも評論文からの出題で、
設問形式は、文章に合わせた語句や語彙の選択問題、語句の意味や
使い方を問う問題などです。

現代文で出題される語句問題は、入試の頻出語句が使われることが多いため、
問題演習で覚えましょう。

主旨をつかむ練習を繰り返し、内容を把握しましょう。

古文は基本問題が多いため、古文単語や文法の意味・使い方を覚えて、
古文の読み方を身につけましょう。

普段使わない熟語やことわざ等が出てくるので「キーワード読解」
「現代文単語」などで現代文の単語力をつけておくことがおすすめです！

出版社：Z会

また、記述力を高めるには「現代文読解力の開発講座」がおすすめです。
解説がとても丁寧なため記述の練習を行う参考書としてとても
おすすめできます！

著者　：霜 栄
出版社：駿台文庫

【まとめ】
法政大学法学部は、試験の傾向を掴んで対策をすれば
かなりの高得点を狙えると思います！

特に英語は配点が高いのでまずは基本的な単語・文法の知識を
つけていきましょう。

また、長文問題が基本のため、英文解釈の力をつけて
正誤問題に対応できるようにしましょう！

皆さんの健闘を祈っています！

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
10/27全国統一中学生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentochu/

11/4全国統一高校生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentoko/

一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE

★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは。
八千代緑が丘校の轟です。

今回は、何が何でも法政大学キャリアデザイン学部に合格したい
という受験生に向けて、法政大学キャリアデザイン学部の
難易度、倍率、傾向、対策法を徹底解説していこうと思います。

「法政大学キャリアデザイン学部に合格したいけど、
　何から始めたらよいか分からない…」という受験生には
是非読んで頂きたいと思います。

【そもそも法政大学ってどんな大学？】
法政大学は、東京を中心に複数のキャンパスを構え、
全15学部を有する私立の総合大学です。

学部数が多いため、幅広い分野の意識を横断的に身につけることができます。
また、グローバル教育も充実しており、世界の課題について論じあう
機会が多いことが特徴的です。

キャンパスは「多摩キャンパス」「市ヶ谷キャンパス」
「小金井キャンパス」の3つがあります。

多摩キャンパス
　経済学部　社会学部　現代福祉学部　スポーツ健康学部　

市ヶ谷キャンパス
　法学部　文学部　経営学部　国際文化学部　人間環境学部　キャリアデザイン学部　GIS（グローバル教養学部）　デザイン工学部

小金井キャンパス
　理工学部　情報科学部　生命科学部

【法政大学キャリアデザイン学部の概要】
法政大学キャリアデザイン学部は2003年4月に創設されました。
キャリアデザインという学部コンセプトは当時日本で最初のものでしたが、
今でもオンリーワンに近いポジションを保っています。

キャリアデザイン学部には「発達・教育キャリア」「ビジネスキャリア」
「ライフキャリア」という3つの領域が存在します。

2年次に自分の最も深めたい領域を専攻し、その領域を軸としますが、
残りの2科目も学びます。

2年次以降、全員が体験型選択必修科目を履修します！
産学連携やボランティア活動など多彩な活動が有り、
事前指導や事後指導も含めて1年間を掛けたインターンシップです！

【入試概要】
受験方式は
①T日程（統一日程）
②英語外部試験利用
③A方式（個別試験）
④大学入学共通テスト利用
の4種類があります。

今回は①T日程　②英語外部試験利用　③A方式について
詳しくお話ししていきます。

＜T日程について＞
T日程の受験科目は以下のとおりです。

・国語または「数学I・Ⅱ、数学A・B」の2科目から1科目　（100点）
・英語　（150点）

※国語は古文・漢文の独立問題は出題しない
※数学Bは数列・ベクトルを出題範囲とする

T日程方式は学部併用が可能なので、
他の学部も気になっている、とにかく法政大学に合格したい
という方におすすめできます！
英語外部試験利用入試と併願もできます！

＜英語外部試験利用について＞
英語外部試験利用の受験科目は以下のとおりです

・国語または「数学I・Ⅱ、数学A・B」の2科目から1科目　（100点）

※国語は古文・漢文の独立問題は出題しない
※数学Bは数列・ベクトルを出題範囲とする

＜A方式について＞
A方式の受験科目は以下のとおりです。

・英語　（150点）
・国語　（100点）
・「数学I・Ⅱ、数学A・B」「世界史探求」「日本史探求」
　「地理探求」「公民（政治経済）」の５科目から1科目　（100点）

一般入試の中で募集人数が最も多いため、学科がもう決まっている方、
学びたいことが明確な方はこちらを受験するのがおすすめです！

【科目別対策法　～英語編～】
まずは英語についてご紹介します。
法政大学キャリアデザイン学部の英語は大問4問構成です。

大問4題とも長文読解問題で、問題数は40問。試験時間は90分です。
長文読解問題は、どの大問も本文量が600語以上で、速読力が必要です。

主に空欄補充問題と語句整序問題で、語彙力や熟語の知識、
空欄箇所前後の内容把握、文法力が問われます。

総合的な英語力が必要なため、早い段階からの対策が重要です。
日ごろから単語帳や熟語帳などを覚え、問題演習を繰り返し、
過去問演習で出題形式に慣れましょう。

全体的に見てみると、正誤問題が多く出題されています。
また、下線部の単語と同じ意味を持つ単語を聞かれる問題も多く見られました。

長文をなんとなくで読み進めてしまうと解けない問題がほとんどです。
長文は一文一文の集まりですから、まずは一文を正確に読めるようにしましょう！
そのためには英文解釈の力が必要不可欠です。

長文が読めるようになりたいけど何からやったらいいかわからない...
という方は『関正生の英文解釈ポラリス[1 標準~応用レベル] 』が
法政大学の英語対策におすすめです！

著者　：関 正生
出版社：KADOKAWA

【科目別対策法　～国語編～】
法政大学キャリアデザイン学部の一般選抜の国語は、
大問3題で構成され、マーク式と記述式併用です。

大問1：現代文　評論（内容説明・空欄補充・内容一致など）
大問2：現代文　評論（空欄補充・内容説明・漢字問題など）
大問3：古文（内容説明・意味問題・文法・内容一致など）

試験時間は60分で、大問2題は現代文、1題は古文の構成です。
各大問で記述式問題が出題されます。
現代文は大問2題とも評論文からの出題で、
設問形式は、文章に合わせた語句や語彙の選択問題、
語句の意味や使い方を問う問題などです。

現代文で出題される語句問題は、入試の頻出語句が使われることが多いため、
問題演習で覚えましょう。

主旨をつかむ練習を繰り返し、内容を把握しましょう。

古文は基本問題が多いため、古文単語や文法の意味・使い方を覚えて、
古文の読み方を身につけましょう。

普段使わない熟語やことわざ等が出てくるので「キーワード読解」「現代文単語」などで
現代文の単語力をつけておくことがおすすめです！

出版社：Z会

また、記述力を高めるには「現代文読解力の開発講座」がおすすめです。
解説がとても丁寧なため記述の練習を行う参考書としてとても
おすすめできます！

著者　：霜 栄
出版社：駿台文庫

【まとめ】
法政大学キャリアデザイン学部は、試験の傾向を掴んで
対策をすればかなりの高得点を狙えます。
特に英語は配点が高いのでまずは基本的な単語・文法の知識を
つけていきましょう。

また、長文問題が基本のため、英文解釈の力をつけて
正誤問題に対応できるようにしましょう！

皆さんの健闘を祈っています！

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
10/27全国統一中学生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentochu/

11/4全国統一高校生テスト開催！詳細・お申込みはこちら！
https://www.jasmec.co.jp/toshin/event/zentoko/

一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE

★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝