誉田進学塾高校部日記

こんにちは。
八千代緑が丘校の轟です。

問題演習の際、
『解答を見れば、「あ～、なるほど」と
　納得するけれど、自力ではなかなか解けない』
ということはありませんか？

また、こんなとき、
『問題を解く量が足りていないのかな…。
　そのうち、慣れて問題を自力で解けるように
　なるだろう…。』
と捉えて、とりあえず、そのまま問題演習を
続けることにする人が多いと思います。

勿論、定着するまでの問題数が足りていない
ということはあります。

ただし、実は理解が十分でなかったり、
問題を解く際の『発想の種』が見つけられなかったり
することが要因かもしれません。

先日、ある生徒から、数学Ⅲの積分の計算問題について
質問を頂きました。

その生徒の悩みは
『積分の計算問題を解く際、
　部分積分を活用して解いたら良いのか、
　それとも置換積分を活用して解いたら良いのか、
　判断ができない。』
ということなのです。

例えば、以下の定積分の計算問題に対して、
瞬時に解き方を思いつけますか？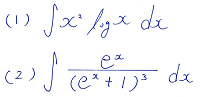

積分の計算に慣れている人は、
解く方針を立てるのに、1秒もかからない
と思います。

今回と次回は、「えっ、すぐには思いつかない…」
という方に是非読んで頂いて、読み終えた際には
瞬殺問題になっていればいいなと思います。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
＜八千代緑が丘　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

＜八千代緑が丘　校舎紹介動画 on YouTube＞
https://www.youtube.com/watch?v=KOoM-l4YrOE

八千代緑が丘校ではいつでも無料で個別学習相談
を行っています。
勉強で困っていることのある方はいつでもおっしゃって下さい。
個別学習相談のお申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

では、今回は、問題を解く準備として、
部分積分と置換積分について、
「そんなのわかっているよ」という方も、
一旦、以下の説明を読んでみて下さい。
後編で解説する際に、必要になりますので。

まずは部分積分について。

次に置換積分について。

では、一旦、部分積分と置換積分について
おさらいをして頂いたところで、
問題の解説は、後編で書かせて頂きたいと思います。

引き続き、後編もご覧ください。

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇
https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm

★Instagram日々更新中★
フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

新規開校！YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは、五井駅前校坪田です！
暑い日が続きますが、皆さん夏バテは大丈夫でしょうか？
塾生にも暑さで体調を崩してしまう人もちらほら....

夏休みももうそろそろ折り返しというところで、
受験生たちにも疲れが見えてきました。
ただし、ここが踏ん張りどころです。
毎日9時登校を続けていけるかどうかが勝負の分かれ目ですね。
以前紹介した演習会Final summerも残り4回です。
ラインキングから自分のライバルを見つけて負けないようにと
頑張っている生徒も....
他にも英単語と熟語では負けないと頑張っている姿もあります。
受験は団体戦、競い合う仲間がいることでやる気につながるのはいいことですね。

1,2年生は部活に追われて忙しそうに過ごしています。
夏休みなのに普段より学校に拘束されていると嘆きも聞こえてきます。
塾に来たら部活の愚痴も夏休みの楽しい思い出も吐き出しつつ、
勉強に向かっているのは素晴らしいことですね。

3年生は長丁場なので休憩をはさみつつ...

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇
https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm
その他、体験・説明会等のお申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

★Instagramはじめました★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＜五井駅前校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pg.htm
校舎紹介動画！YouTube公開中👇
https://youtu.be/Y9YyD6KE_NA
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは。土気駅北口校の吉澤です。

夏休みで勉強時間が普段より取れるようになったからか、生徒からの質問・相談も増えてきました。

その中で「苦手な科目を勉強する気になれない」という相談がありました。
今回はこのことについて書きたいと思います。

皆さんそれぞれに苦手にしている科目があると思います。
確かに、苦手科目を勉強するのは楽しいことではないかもしれません。
ただ、苦手だからと後回しにしてしまうのはもったいないなと思います。
苦手な科目ほど伸び代があり、全体の得点を上げられる科目です。
そのため、前向きに苦手科目を取り組んでほしいです。

とは言っても、苦手な科目をどう勉強したら良いか分からないという声も出てくると思います。
その場合、まずは得意科目の勉強法を使えないか試してみましょう。
得意になった理由には勉強方法が合っていた可能性もあります。
同じ方法で勉強できそうなら、これほど都合の良いことはありません。

同じ勉強法が使えなかった場合は苦手科目に触れる時間を増やしてみましょう。
苦手な理由には単純に勉強時間が足りてない可能性もあります。
また、触れる機会が増えることで苦手という意識が薄れることがあります。（心理学では単純接触効果なんて呼びます）
他の科目と並行しながら、勉強時間の割合を増やしていきましょう。

なぜ、この時期に苦手科目について書いたかというと、
苦手科目は残しておくと入試直前期のメンタル面に響くからです。
苦手科目を克服できなくても、やるべきことはやったという気持ちで入試に挑んでほしいです。

「最後に苦手科目をやれば良いんでしょ！」と思うかもしれませんが、
入試直前期に苦手科目ばかりに時間を割いていると他の科目の勉強時間が減ってしまいます。
入試直前の皆さんの脳は水が並々注がれたグラスのごとく、知識が限界ギリギリまで詰まっています。
その時期に一科目集中の勉強方法を取ると、他の科目の知識が零れ落ちてしまいます。
私としては直前ほど満遍なく勉強することをオススメします。

そういった意味でも、時間の取れるこの時期に苦手科目の克服に取り組んでもらいたいです。
この夏の頑張りは皆さんの学力を大いに飛躍させます。苦手科目もあわせて伸ばしていきましょう。

（土気駅北口校　吉澤）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇
https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm
その他、体験・説明会等のお申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★Instagramはじめました★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
＜土気駅北口校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pt.htm
校舎紹介動画！YouTube公開中👇
https://www.youtube.com/watch?v=80303E47nz8
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは！
ユーカリが丘校の松浦です。

今回は9/10(日)に予定されている進学相談会「大学進学フェスタ」のご案内です。

各大学で現在オープンキャンパス真っ盛りだと思います。
大学のキャンパスを実際に訪問していろいろなお話しを聞けるのは最大のメリット。
でも、ほとんどの大学は予約制。キャンパスもあちこちにあるので行くとしても一日がかりです。

その点、進学相談会では身近な会場に各大学の入試広報の先生がたが来てくださります。
ブースで１対１で相談できますし、パンフレットを集めるだけなら短時間でたくさんの大学のパンフレットを手に入れられます。

「でも何を聞けばいいか分からない…」という人も多いと思います。
大丈夫です。お越しになっている先生方はそういうみなさんの対応に慣れている説明のプロです。
「まだやりたいことが見つからないんです」とか「どんな勉強をすれば入れますか」といった質問でも丁寧に対応してくださりますよ。

「受験までまだだいぶ先だから受験生でもないのに行ったら気まずい…」
大丈夫です。ここだけの話、大学の先生方は、それこそ中学生小学生の方のほうが気合が入るそうですよ。だって、受験生はもう志望校とか進路とか決まっているから。まだこれから進路を考える生徒のほうが、説明しがいがあるそうです。

是非この機会にご参加ください。先着順の受付となっていますので、お申込みはお早めに！

(ユーカリが丘校　松浦)

★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇
https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm

こんにちは！
おゆみ野駅前校事務の堀内です！

ついこの間夏休みに入ったと思ったら、8月はもう5日経ちました。
時間の経過は早いですね。
ボーッと過ごしていたらあっという間に始業式でした、とならないように気を付けましょう！

連日猛暑が続きますが、みなさん体調は崩していませんか？
熱中症警戒アラートも発令されており、危険な暑さと言えますね・・・。
そんな中登校している皆さんはすごいです！
受験生は毎日登校が当たり前と言われていますが、歩いているだけでめげそうな暑さの中、
朝9時から登校していて本当に偉いと思います！！
1、2年生でも朝9時に登校している生徒もおり、
夏にしっかり学習するぞ、という気合が伝わってきます！

校舎で快適に過ごせるようにしっかり温度調整して、みなさんをお待ちしています♪
この夏でほかのライバル達に差をつけちゃいましょう！！

（おゆみ野駅前校事務　堀内）
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇

https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm

その他、体験・説明会等のお申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm

★Instagramはじめました★

フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜おゆみ野駅前校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/poy.htm

校舎紹介動画！YouTube公開中👇
https://www.youtube.com/watch?v=dgfx1ijTSiA

こんにちは。
八千代緑が丘校事務の牛尾です。

８月も１週目が終わろうとしていますね。
皆さんと校舎で過ごす１週間はあっという間だなぁと
日々感じています。

講習生の皆さんは、自分で立てた学習計画に沿って
しっかり登校できています。
中には、朝９時に登校して学習を進めている生徒さんも。
今のうちに、朝から勉強する習慣をつけていくことは
非常に素晴らしいことです。この調子で頑張っていきましょう。

高１・高２生の皆さんは、部活等で忙しい中でも時間を見つけて
学習を進めていますね。
「旅行に行くまでに、ある程度進めておきたくて！」と、
頑張っている生徒さんもいらっしゃいます。
目標や楽しみがあると、より一層頑張れますよね。
気分転換をすることも大切。
やるときはやる！とうまく気持ちを向けていきましょうね。

高３生は「Final Summer」の第11回が終了しましたね。

毎朝９時登校、午前中は演習を受けて、午後は閉校まで学習を進める。
皆さん、本当によく頑張っているなぁ…と思います。
毎日、お疲れ様です。
まずは、毎日頑張っている自分を沢山褒めてあげてくださいね。

そろそろ疲れが溜まってくる頃ですよね。
休む時間も大事に出来ていますか？

運動や身体を使う作業を休憩も取らずにしていると、
力が入らなくなったり、ふらふらしてきたりしてしまいます。
勉強もそれと同じ。ずっと頭を使い続けていると、
疲れやストレスが溜まってケアレスミスが増えたり、
思考が働かなくなってしまいます。
そんな状況で学習を進めるのは効果的ではありません。
集中力の回復には、休憩が大切になってきます。

例えば、自分が集中できる時間に合わせて休憩をとったり、
少しストレッチをしてみたり。色んな休憩方法がありますよね。
自分が、これなら頑張れるかも！と思える休憩方法を見つけて
是非実践してみてください。

また、校舎には休憩スペースがあります。

食事をするときだけでなく、少し疲れたから
小休憩しようかな…なんて時でも使っていただいて大丈夫ですよ。

勉強⇔休憩を適切に切り替えて、学習を頑張っていきましょう！
（八千代緑が丘校　牛尾）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇

https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm

★Instagramはじめました★
フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

新規開校！YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

こんにちは。
八千代緑が丘校の轟です。

東進衛星予備校では、生徒一人ひとりが映像授業で
学習していますが、週に１度、ＨＲという形で
みんなで集まって、顔を合わせる機会があります。

最近入塾したばかりのＡくんからは、
「東進でもみんなで集まる機会があるんですね!!」
と、とても新鮮な表情で言ってくれました。

そんなＨＲですが、せっかくみんなで集まったのですから、
ただ、一方的に話を聞くだけの場だともったいないですよね。

そこで、同じ塾生仲間同士、交流もかねて、
みんなで一緒に考える時間も設けています。

今週はいくつか英語のクイズを行ったのですが、
そんな中の一問をご紹介致します。

今週のＨＲでも、みんなで一緒に
英語のクイズを考えてみました。

括弧に入る英単語は①～④のうちどれ？

A:I think I am going to ( )
the job at the bank.

B:That is great. You will get some
good experience working there

① connect　② accept　③ translate　④ imagine

ＡさんとＢさんのこの会話、
何となくでも、どのような意味の会話なのか、
わかったかもしれません。

また、選択肢の英単語も基本的なものですが、
生徒たちは、なかなかすんなり選択肢を選べません。

「じゃぁみんな、これだと思った番号を
　手を挙げて指で教えてっ」
と言うと、みんな思い思いの番号を示してくれました。

acceptは「(申し出、招待、提案など)を受け入れる」の意味で、
「accept the job」を直訳すると「その仕事を受け入れる」
となりますが、「その仕事を受け入れる」だと何だか
ピンと来ないですよね。

「その仕事を受け入れる」とはつまり、
「その仕事をすることになる」という解釈になるわけです。

このように解釈するためには、単に
『〇〇という単語の意味は□□です』
という覚え方では不十分です。

その単語がどのようなニュアンスを持った英単語で、
どのような場面で、どのように使われるのか、
例文も合わせて理解して頭に入れておくと、
使われている文の文脈に合わせて臨機応変に
解釈できるようになっていくと思います。

そう考えると、英単語の覚え方一つでも、
その先の英語の力の伸び方に差が生じそうですね。

英単語１つ覚えるにしても、
奥が深いねと生徒たちと話をした今週のＨＲでした。

（八千代緑が丘校　轟）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★9/10(日)開催！『大学進学フェスタ in CHIBA』参加申込受付開始！★

👇👇👇参加申込はこちらから👇👇👇
https://www.jasmec.co.jp/toshin/event/shingakufes/shingakufes.htm

★Instagram日々更新中★
フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜八千代緑が丘校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pym.htm

新規開校！YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

みなさん、こんにちは。
五井駅前校の富田です。

8月になり、夏休みもあっという間に過ぎようとしています。
現在校舎では夏期特別招待講習を頑張っている一般生の皆さんが
毎日校舎に登校して学習しています。

さて、本日は少し英語の学習についてのお話です。

よく生徒からこんな質問を受けます。
「英語はどうやったら点数取れるようになりますか？」と。

その答えはズバリ、「まずは単語と熟語から」やる！ということです。
英語の学習は言語ですから、まずルールを覚えることと語彙力が
カギになります。

小学生の時に漢字練習をしたり、小さい頃いろんな言葉を覚えた
のと同様です。

英語のルール＝文法と定義するならば、いくらルールをしっかり
覚えても日本語で何と訳すのか分からなければさすがに理解する
のは難しいと思います。

だからこそ、日々の学習の中で単語や熟語を勉強することはとても
大切なんです。

premium高校部では、東進のコンテンツである「高速基礎マスター」
を使って語彙力の学習を実施しています。

これは高校2年生のホームルームで昨日特訓会を実施した様子です！

単語や熟語は覚えてもすぐ忘れてしまうもの・・・かもしれません。
受験生の昼休みの過ごし方を見ていると、ご飯を食べながらボロボロ
になった単語帳を開いたり、スマホを使って高速マスターをやって
いる姿をよく見かけます。

志望校合格を勝ち取るその日まで、毎日英単語・熟語の学習は欠かせ
ないものなのです。

人間は忘れてしまうもの、だからこそ反復練習が必要です。

8/5（土）より、premium高校部では夏の英単語特訓としてこの
高速基礎マスターを使って英単語の学習を強化できるイベント
を開催しています！
詳細は校舎までお問合せください。

日数は限られていますが、この機会にぜひ、英語の得点力アップに
力を入れてみませんか！？

学習フォローは校舎スタッフが丁寧に行います。
是非、お問合せください！

（五井駅前校　富田）

★Instagramはじめました★

フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜五井駅前校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pg.htm

校舎紹介動画！YouTube公開中👇
https://youtu.be/Y9YyD6KE_NA

こんにちは、鎌取駅南口校の小井塚です。

ほとんど毎朝、受験生は、
塾の演習テストであるFinal Summerを受験しています。
この夏は受験の天王山、とにかくやるっきゃありません。

皆さん、準備をしてきており、真剣に受験しています。
夏休みほど時間が取れる期間はありません。
今が踏ん張りどきです！

午後にはランキングが掲示されます。
他の校舎の受験生の様子がわかるこの掲示は、
生徒にとって、刺激になっています。
「自分も負けてられない」と感じる気持ちが大事です。

8/20には共通テスト本番レベル模試があります。
まずはそこで結果を出すため、
そして受験生全員が充実した夏を過ごせるよう
スタッフ一同、全力でサポートしていきます。

（鎌取駅南口校　小井塚）
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★Instagramはじめました★

フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜鎌取駅南口校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/pk.htm

2号館開校！YouTubeはこちらから👇
https://youtu.be/JRUQDrQOE5U
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

大網白里校の一関です。

タイトルにもありますが、間もなく夏休み開始から2週間！という方が多いかと思います。
例年になく暑い夏ですが、体調は万全でしょうか？？？

大網白里校では、受験生はもちろん、高1生、高2生も連日校舎
に登校し、映像授業をどんどん進めています！

高1生、高2生の学習ペースを保つ意味でも、学年ごとにホームルームを行い、週の学習計画を立て、実行に向けて行動しています。

それ以外にも大学学部紹介なども行っていますが、今週のホームルームでは「英単語」の重要性についてお伝えしました。

単純な文法問題ですが、皆さん正答は分かるでしょうか？
この英単語、実は…

東進高速マスター単語1800で学習できる単語になります。
塾生はこの夏、英単語・英熟語の重要性を意識し、十分な
語彙力を身につけることも目標にしています。

塾に通っていない皆さんは、毎日英単語・英熟語に触れられているでしょうか？
不安！という方には朗報です。

「英単語集中特訓　5日間体験」というイベントを8月5日（土）から申込受付予定です。
詳細は当日5日、東進ホームページでチェックしていただきたいのですが、まさにこの夏、英語の土台を固めるのにぴったりな機会になります。気になる！という方は校舎までぜひお問合せください！

まだまだ8月が始まったばかり！
充実した夏にしていきましょう！
（大網白里校　一関）
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
★Instagramはじめました★

フォローお願いします👇
https://www.instagram.com/honshin_premium/

＜大網白里校　校舎紹介ページ＞
http://www.jasmec.co.jp/koushaguide/po.htm

校舎紹介動画！YouTube公開中👇

https://www.youtube.com/watch?v=VIFie-0hLP4
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝