こんにちは。
八千代緑が丘校 轟です。
夏期講習期間に入り、大学の個別試験の過去問を
解き始める生徒が多くなってきました。
今日はAくんから、数学の質問がありました。
問題は2020年の京都大学 文系数学 前期の第5問です。
こちら↓。
***********************************************
縦4個、横4個のマス目のそれぞれに1,2,3,4の
数字を入れていく。
このマス目の横の並びを行といい、縦の並びを列
という。
どの行にも、どの列んも同じ数字が1回しか現れない
入れ方は何通りあるか求めよ。
下図はこのような入れ方の一例である。
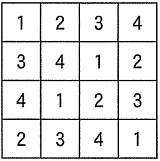
**********************************************
まだ、難関大学の入試問題を解きなれていないこともあり、
どのように手をつけていって良いか、最初の一手を
思いつくのが困難だったりしますよね。
ここでAくんへのアドバイスは
『まずは簡単な数字から問題を解きほぐしてみよ!』
というところです。
例えば、2行2列だった場合はどうなるか?
次に、3行3列なら?
そして、いよいよ4行4列ならどうなるか?
といったように、小さい規模から大きい規模へと
段々と拡張していくのは有効な手です。
特別な計算の技法などは必要ない問題ですので、
ぜひ、クイズを解く感覚で解いてみては
いかがでしょうか?


さて、夏期講習期間と言えば、塾生は
共通テスト対策にも取り組んでいます。
共通テストの数学ⅠAの過去問を解いている受験生、
上記の京都大学の入試問題、どこか似た雰囲気の問題を
解いた経験、ありませんか?
こちら↓
最近解いたという受験生は「ピン」と来たかもしれないですね。
そう、2022年の大学入学共通テストの数学ⅠAの本試験の問題の
第3問(場合の数・確率)の問題です。
『えっ!? どこが似ているの?』
と思った方が多いかもしれません。
この2題は、どちらも同じアプローチで
解くことができます。
(このアプローチを使わなくても
解くことができます。)
さて、この2題の背景となる問題を
皆さん、ご存知でしょうか?
数学ⅠAの教科書の発展的内容のところで、
紹介されているかもしれません。
良かったら、改めて数学ⅠAの教科書を見てみて下さい。
では、背景となる問題については、明日のブログで
ご紹介致します。
よろしければ、明日も合わせてご覧ください。
(八千代緑が丘校 轟)
=======================
一日体験の詳細・お申し込みはこちら!
https://www.jasmec.co.jp/toshin/event/taiken/
<八千代緑が丘校 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
★Instagramもやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
=======================

