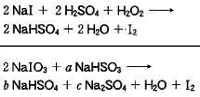こんにちは。
八千代緑が丘校の轟です。
早いもので共通テストから1週間が経過しました。
今回は、共通テストの化学を解いてみて、
その振り返りをブログで書かせて頂きたいと思います。
難易度については、大学入試センターの
平均点を見ると、昨年の平均点が54.8点だったのに対し、
今年の中間発表では47.7点だったので、
客観的に見て、難化したと思います。
(知り合いの化学の先生の感想では、昨年も十分に難しかったため、
昨年とそんなに変わらないという意見はありました。)
ただ、今回で共通テスト5年目を迎え、改めて感じることは、
問題の作り方が個別試験に近いなというのが率直な感想です。
以前のセンター試験の際には、センター試験の問題と言えば、
いかにも教科書コテコテの題材だけれど、選択肢の作り方が
工夫されていて、ミスをしやすいという傾向があり、
『選択肢を間違えずに選ぶ』というところにポイントが
あったように思います。
一方、共通テストに関しては、問題の題材自体が難しいと
いいますか、普段見慣れていない題材が出題されるように
なった点が大きく異なると思います。
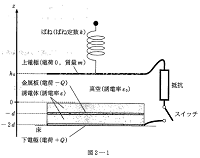
例えば、第3問の問4でヨウ素の生成・製造についての問題が
出題されましたが、生徒たちの話を聞いていると、学校では
扱わない内容が出題されたのは、一例だと思います。
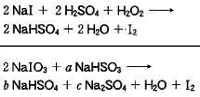
普段、あまり扱わない題材をテーマにして、
導入で説明を加えて、反応式でヒントを与えて、
「この反応式があれば、反応量計算はできますよね」
と係数を使えばいいだけだからとか、濃度計算やればいい
だけだからみたいな問題が増えたと感じています。
このような問題に対する対応の仕方と言うと、
試験までに経験してきた様々な題材の問題を解いた
経験を活かして、「ちょっと変わった話をしているけれど、
普段通りの考え方の手順で対応してみよう!」
と思えるかどうかが大事です。
そう考えると、試験では理科2科目必要でそのうちの
1科目が化学だけれど、もう片方の理科科目の学習に
偏っていて、化学の学習が手薄(経験値が少ない)という
受験生にとっては、共通テストの化学はとても難しく
感じると思います。
また、別の視点で見ると、個別試験で使う解法を
使って解く問題が増えたと思います。
例えば、第1問の問3の二酸化炭素の溶解度の問題や
第1問の問5-bの浸透圧の問題が一例です。
「解法を知らないと、何をしていいのかわからない」
という受験生は感じると思います。
共通テストのなってから、思考力が問われるようになった
というフレーズをみなさんも耳にしたことがあるかも
しれませんが、化学や物理に関しては、個別試験と同様に、
どの解法を活用してその問題を解くか、ちゃんと判断が
できるかが試されていると思います。
解法のパターンというのがいくつかあり、
まずはそれをしっかりと頭に入れて頂いて、
問題を見たら、頭の中にある、どの解法で解くのか
を判断して、その解法に沿って問題を解き進めていくと、
答えが出るという感覚で問題を解いて頂くと良いかなと思います。
センター試験から共通テストに移行したことで、
頭の中にそろえておく解法パターンが増えたと思います。
だから、センター試験から共通テストに移行して、
難易度が上がったのは必然的なのでしょう。

普段、生徒たちから、「化学のお薦めの問題集はありますか?」
とご相談を頂いた際に、バンバンお薦めしている問題集が
上の写真の『化学の解法フレーム』という問題集です。
著者 :首藤大貴、犬塚壮志
出版社 :かんき出版
(以前、発売したタイミングで、こんな問題集がありますと
ブログでご紹介させて頂いたことがありました。↓)
https://www.jasmec.co.jp/cgi-bin/blog-diary-open1/diary02/blog-diary-open2.cgi?no=3953
生徒たちに、自信を持って紹介している手前、どれだけ
有効かなと、今回の共通テストの問題と照らし合わせて
確認してみました。
結論から言えば、生徒たちにお薦めして良かったなと
感じています。
例えば、先にも紹介させて頂いた第1問の問3の二酸化炭素の溶解度の問題
(ヘンリーの法則を活用して解く問題)においては、解法フレーム 理論編の
260ページの『フレーム50』に、そのまんま、解き方が掲載されています。
この問題において、東進の答案再現の集計によると、
受験生の正解率は43%でした。
解法フレームの『フレーム50』をやって、それを覚えていたら解けたのに…。
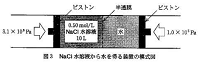
また、第1問の問5-bの浸透圧の問題においても、解法フレーム 理論編の
300ページの『フレーム58』に掲載されています。
密閉されたところに両側ピストンで圧力をかけて、その時のその力の関係が
どうなるかってということを知らないと、解き方として関係式1個
作れないんですね。
逆に知っていれば、計算自体は複雑ではないので、
瞬殺問題になります。
東進の答案再現の集計によると、この問題の受験生の正解率は
なんと、12%でした。解法フレームの『フレーム58』をやって、
それを覚えていたら、瞬殺問題だったのに…。
また、第3問の問2のケイ酸ナトリウムの生成については、
解法フレーム 無機化学・有機化学編の89ページの『フレーム17』で
ガッツリと解法を扱っています。
東進の答案再現の集計によると、この問題の受験生の正解率は44%
でした。
そして、第4問の有機化学の大問では、今年は天然有機物の問題が
全然出題されませんでしたね。
昨年、ガッツリ出題された影響でしょうか…。
その分、今年は合成高分子の問題が沢山出題されました。
この合成高分子に関する計算問題がネックになった受験生は
多かったのではないかと思います。
第4問の問4-bでビニロンに関する問題が出題されましたが、
解法フレーム 無機化学・有機化学編の306ページの『フレーム32』
で反応の解き方がしっかりと掲載されており、そこをしっかりと
理解し、頭に入れておけば、その次の応用問題の問4-cも解けたと
思います。
『フレーム32』をしっかりと抑えておけば、問題番号25-28の
「7点は頂き」というところでした。
ちなみに、問4-cにおいては、東進の答案再現の集計によると、
受験生の正解率は34%という結果でした。
第5問は毎年、総合問題という形式ですが、
今年は原油(石油)の題材が出題されました。
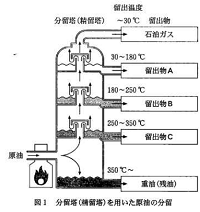
この問題はネットのニュースでも話題になっていましたね。
例えばこちら↓
https://news.yahoo.co.jp/articles/de2de2d97dbf6013f90bd4577a15545e795e075a
ただ、↑のネットニュースに『「ほぼ東大化学」「理不尽」受験生から悲鳴も』
というタイトルが付いていましたが、これはちょっと盛り過ぎというか、
いかにも、閲覧数を増やすような過剰なタイトルの付け方だなと思いました。
題材そのものは、個別試験の題材と一緒になってきていますし、
センター試験と比較して、難易度が上がったことは確かです。
ですが、いくら、東京大学で過去に扱った題材と一緒だったとしても、
設問の難易度は、さすがに、そこまで言う程は難しくありません!
志望校にもよりますが、国公立大学/私立大学の個別試験では
出題される題材であるため、個別試験対策をしている受験生に
とっては、ビックリするような問題ではなかったと思います。
ただ、難関大の入試問題に寄せていることは確かだと思います。
題材は難関大と一緒で、その題材の入り口を問われるという
問題が出題されているなと思いました。
ですから、センター試験時代のときは、学習する順番として、
各科目、一通りインプットを終えたら、個別試験の過去問を解く前に
まずはセンター試験で基礎レベルの問題を解けるようにして、
それから個別試験対策を行うのが一般的だったと思います。
しかし、物理・化学に関して言えば、日本大学や千葉工業大学、
東洋大学の個別試験の問題よりも、共通テストの問題の方が
難しいです。
そのため、私立大学で言えば早慶上理、、
国公立大学で言えば旧帝国大学・東京科学大学
を目ざす受験生はいきなり共通テストの過去問を解いてみて
良いと思います。
しかし、そうでない受験生は、いきなり共通テストの
問題を解く前に、志望校よりも少し難易度の易しい入試問題から
解き始めて、私立大学で言えば、MARCHの過去問と共通テストの
問題を併行して解く、国公立大学で言えば、例えば千葉大学志望の
受験生であれば、千葉大学の過去問と共通テストの過去問を併行して
解く順番が良いように思います。
(注意:あくまでも物理・化学に関しての話です。)

今回は、共通テストの化学の問題を振り返りつつ、
共通テストの化学とはどのような傾向の問題なのか
という話を書かせて頂きました。
新高校3年生に、ご参考にして頂ければと思います。
(八千代緑が丘校 轟)
=======================
2/1河合正人先生特別公開授業!詳細・お申し込みはこちら!
https://www.jasmec.co.jp/toshin/event/kokaijugyo/
新年度特別招待講習受付中!詳細・お申し込みはこちら!
<新高3、高2、高1、高0>
https://www.jasmec.co.jp/toshin/event/shotaikoshu/
一日体験の詳細・お申し込みはこちら!
https://www.jasmec.co.jp/toshin/event/taiken/
<八千代緑が丘校 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
<八千代緑が丘校の校舎紹介動画はこちら👇>
https://youtu.be/KOoM-l4YrOE
★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
=======================