こんにちは。
八千代緑が丘校の轟です。
2022年も残すところあと1日。
年末はいかがお過ごしでしょうか?
学校から宿題がたくさん出されている学校もあり、
生徒たちを見ると、学校の課題にも頑張って
取り組んでいます。
今日は、生徒から図形の問題で質問を頂いたのですが、
今まで多く頂く質問の題材でしたので、
同じところでつまづいている高校生が多いかも
しれないと思い、ブログにしてみました。
生徒からの質問は、このような問題でした。
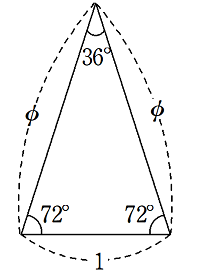
『頂角が36度の二等辺三角形の底辺の長さが
1であるとき、等辺の長さを求めよ。』
「中学校の頃、相似の単元が得意で、
今でも覚えているよ」という方はいいのですが、
「中学校の頃から図形が苦手…」という方にとっては
数学Ⅰの「図形と計量」や数学Aの「図形の性質」は
つらい単元ですよね。
この問題の解説を、簡単に書いておくと、
以下となります。
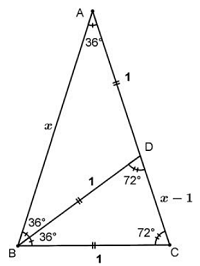
上図のように三角形ABCにおいて、
底角∠ABC の二等分線と辺CAの交点をDとすると
三角形BCDも頂角が36度の二等辺三角形となるんです。
つまり、三角形ABC∽三角形BCDという相似な
三角形が見えてくるわけなんです。
AB : BC=BC : CD
x : 1=1:(x-1)
x^2-x-1=0 ……①
式①の2解のうち、正の値が求める解となり、
x = (1+√5)/2
となります。
=================================
<八千代緑が丘 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
<八千代緑が丘 校舎紹介動画 on YouTube>
https://www.youtube.com/watch?v=KOoM-l4YrOE
八千代緑が丘校ではいつでも無料で個別学習相談
を行っています。
勉強で困っていることのある方はいつでもおっしゃって下さい。
個別学習相談のお申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm
=================================
この問題、実は『黄金比』という
有名な題材なんです。
ここで「黄金比」と聞いて、
名前だけは聞いたことがある
という方は多いかもしれません。
ただ、「黄金比って何ですか?」
と聞かれると、答えにつまってしまう
という方は多いのではないかと思います。
そこで、今日は『黄金比』について
簡単に触れたいと思います。
黄金比の定義の仕方はいろいろあるのですが、
直感的に分かりやすい長方形による定義を
今回はご紹介したいと思います。
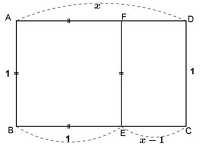
上図において、長方形ABCDから正方形ABEF
を切り取ったものが長方形ECDFです。
長方形ABCDと長方形ECDFが相似となるのは
長方形の辺の比がどのような場合でしょうか?
AB=CD=1, BC=AD=x とおくと
長方形ABCD ∽ 長方形ECDF ですから
AB : AD=EC : CD
1 : x=(x-1):1
x^2-x-1=0 ……①
というように先に出てきた式①に帰着されます。
式①の2解のうち、正の値が求める解となり、
x = (1+√5)/2
となります。
短辺と長辺の比が 1 : (1+√5)/2
となる長方形を黄金長方形(Golden rectangle)
と呼びます。
また、この比の値 1 : (1+√5)/2 を黄金比(Golden ratio)
と呼びます。
ちなみに、最初に登場した
頂角が36度、底角が72度である二等辺三角形を
黄金三角形(Golden triangle)と呼びます。
また、学校の課題や定期試験で
よく正五角形を題材にした問題が出題されます。
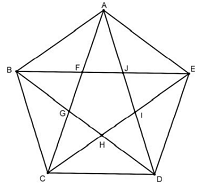
上図のような正五角形(pentagon)において
対角線を全て描くと五芒星(pentagram)が得られます。
ここで、1辺の長さが1の正五角形の
対角線の長さを求めてみます。
上図においてAB=1、BE=x とおくと
三角形ABE ∽ 三角形JEAですから
AB : BE=JE : AE
1 : x=(x-1):1
x^2-x-1=0 ……①
というように先に出てきた式①に帰着されます。
式①の2解のうち、正の値が求める解となり、
x = (1+√5)/2
となります。
すなわち,正五角形では
1 辺の長さと対角線の長さの比が黄金比
となっています。
それから、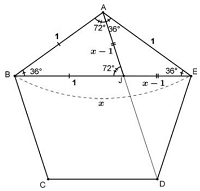
EJ=BE-BJ=(1+√5)/2 -1=(1-√5)/2
であるため、
EJ : BJ=(1-√5)/2 : 1 = 1 : (1+√5)/2
よって,正五角形の2本の対角線は、
それらの交点において黄金比に内分される
ことが分かります。
ですから、よく見る頂角が36度、底角が72度
である二等辺三角形の底辺と等辺の比も
正五角形の一辺の長さと対角線の長さの比も
同じく1 : (1+√5)/2 と黄金比に
なっているわけなんですね。
あまりにも多く登場する題材ですので、
良かったらご参考にしてみて下さい。
では、良いお年をお迎えください。
(八千代緑が丘校 轟)
=======================
★共通テスト同日体験受験★
お申込みはこちらから👇
https://www.jasmec.co.jp/toshin/event/dojitsu/index.htm
★冬期定例入塾説明会★
お申込みはこちらから👇
https://www.jasmec.co.jp/toshin/event/setsumeikai/index.htm
★冬期特別招待講習★
お申込みはこちらから👇
https://www.jasmec.co.jp/toshin/event/shotaikoshu/index.htm
★Instagramはじめました★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
<八千代緑が丘校 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
新規開校!YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
=======================