★千葉中央駅校開校!Instagramはじめました★
フォローお願いします👇
https://www.instagram.com/premium_chibachuou
大学受験のあれこれを投稿していきます☆
=======================
こんにちは。
八千代緑が丘校の轟です。
最近は定期試験直前の生徒が多く、
生徒たちが定期試験に向けて
学校のワークなど、問題演習に励んでいます。
今日は生徒から化学の質問を受けました。
高校生に入って、化学で最初に難しさに直面するのは
モル(mol)だと思います。
そもそもモル(mol)の大小が、
原子や分子の粒子の数の大小を表している
ことを理解するのも難しいですよね。
今日は『飽和蒸気圧』に関する問題の質問でした。
『飽和蒸気圧』って中学校の理科でも習いますが
わかっているようで、実はイマイチよくわかっていない
という人は結構多いのではないかと思います。
(実は、私が高校生の頃に理解するのに苦労した分野の
1つだったんです。)
では、ウォーミングアップに、
以下のクイズを考えてみて下さい。
『ピストン付の容器に気体が閉じ込められています。
温度を一定に保ち、を蒸気圧曲線の地点A ⇒
地点B ⇒ 地点Cと変化するように気体にかける圧力を
徐々に増していきました。
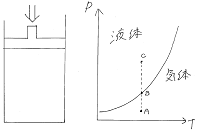
このとき、縦軸を体積V、横軸を圧力PのP-Vグラフ
がどのように変化するか描いて下さい。』
===========================
<八千代緑が丘 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
八千代緑が丘校ではいつでも無料で個別学習相談
を行っています。
勉強で困っていることのある方はいつでもおっしゃって下さい。
個別学習相談のお申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm
===========================
では、クイズの解説をしていきます。
地点A ⇒ 地点Bに変化する際は、
気体の状態のまま変化するため、
状態方程式:PV=nRT (= 一定)
に従って変化しますね。
つまり、PVは反比例のグラフを描きます。
地点Cに達すると、気液平衡(つまり、気体と液体が共存
している状態)となります。
つまり、地点Cでは気体が完全に液体に変化しきるまで
気体の圧力は飽和蒸気圧に保たれています。
よって、グラフは圧力が一定のまま、気体の体積が
小さくなっていきます。
(気体から液体に変化するので、気体は減っていく、
つまり、気体の体積は小さくなっていきます。)
状態の変化を絵に描くと↓のような感じです。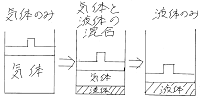
そして地点B ⇒ 地点Cに変化する際は、
気体の体積は0で、圧力が増えていきます。
ですから、解答のグラフは↓のようになります。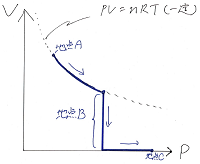
他にも、圧力を一定に保ったまま、温度を下げて
いった際のTVグラフや、
体積一定で、温度を下げていった際のTPグラフなど
練習のために、描いてみて下さい。
また、蒸気圧曲線の問題と言えば、
水は常温でも蒸発して、蒸発した気体は
水蒸気圧の値となっていることに気を付けて下さい。
例えば、下のような図が与えられていて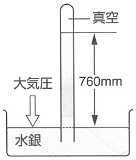
「水銀の代わりに水を用いると、水柱は何mになりますか?
ただし、水銀の密度は13.6g/cm^3、水の密度は1.0g/cm^3
大気圧は1.01*10^5Pa、水の飽和蒸気圧は
3.00×10^3Paとする。」
といったように、問題文中に飽和蒸気圧の値が出されていたら、
「あっ、これは水が蒸発して水蒸気になっているな。
そして、その水蒸気の圧力は飽和水蒸気圧の値に
なっているな」というように気が付けると
今回の定期試験の化学、点数が少しでも上がられるかも…。
(ちなみに、上記の問題設定だと、答えが9.96mになります。)
あともう少しで定期試験を迎えますが、
頑張って乗り切っていきましょう。
応援しています!!
(八千代緑が丘校 轟)
=======================
★一日体験・個別説明会受付中!★
詳細・お申込みはこちらから👇
https://www.jasmec.co.jp/toshin/reserve/premium_reserve.htm



















