おはようございます。
八千代緑が丘校の轟です。
以前、今年の東京大学 理系数学と物理の
問題を解いて、ブログで好評を書かせて頂きました。
ただ、まだ、私の解いた解法と、他の方の解法を
比較していなかったため、今更ではありますが、
東進の解答速報では、どのような解法が
掲載されているかなと気になり、
確認してみました。
どの先生が解答速報を作成されたのかは
わからないのですが、
「この問題は概ね解き方が一緒だなぁ」という
問題や、「なるほど、こうやって解いたのね~」
と思う問題がありました。
(それは必然的ですが…。)
ただ、気になったのは第6問の複素平面の問題。
問題はこちら↓。

(1)と(2)はいいとして、(3)で掲載されている
解法は、勿論、正しいのですが、
「なんで、こんな、手間のかかる解法を
掲載しているんだろう!?」
と思ってしまいました。
東大同日体験受験を受験した新高校3年生の
答案を見ると、私が確認した範囲では、
塾生の中で第6問を完答できた生徒はいませんでした。
ですから、おそらく既に東進の解答速報を通して
復習したと思いますが、あの解法では復習しづらく
なかったですか?
あまりにも、掲載されている答案は微妙だなぁと
思ったので、今回、ブログで別解をご紹介したいと
思います。
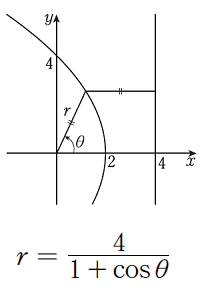
私は、(3)は極方程式を活用して解きました。
極方程式を活用すると、詳細は省きますが、
(2)で求めた放物線上の点を
以下のように表現できますね。
更に
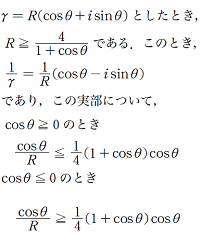
という感じで、1/γの実部の最大値と最小値を
簡単に求めることができます。
解答を詳細には書いていませんが、
↑を参考にして、気が向いたら、
自分なりに答案を作ってみて下さい。
(3)を、東進の解答速報のように、
γ=x+yi(x,y∈ℝ、iは虚数単位)とおくのは
新高校3年生にとっては、その方が発想しやすいかも
しれませんが、それにしても、その後の処理の仕方も
イマイチというか、もっととっつきやすい処理の仕方が
あるのになぁと私は思ってしまいました。
ちなみに、数学の先生や、数学についての知識が多い
大人の方だと、(3)の問題を見ると、ニヤニヤしながら
解いていそうです(笑)
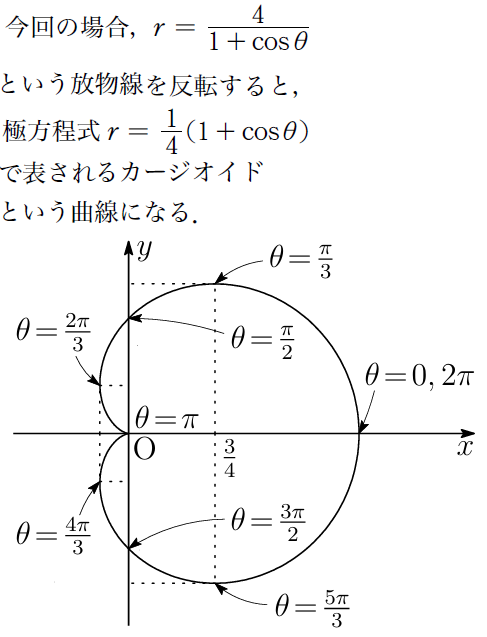
なぜかと言うと、極を焦点に持つような放物線を
反転すると、カージオイドになります。
ですから、(3)は、『1/γがカージオイドの周および内部を動くとき、
x座標の最小値と最大値を求めよ』という問題と同値なんですね。
ですから、カージオイドの式において、θ=2π/3の時に最小値、
θ=0のときに最大値をとることにすぐに気が付いてしまうので、
瞬殺問題となります。
でも、こんなこと、高校生は知らないですよね!?
(知っている高校生がいたら、よく学習していると感心します。)
というわけで、今年の東京大学 理系数学の題6問は
2024年、2023年の第6問と比較すると、随分と解きやすい
問題が配置されていたので、今年、受験された方は
最後に少し安心して取り組めたのではないかと思います。

では、今日も皆さん、良い学びとなりますように~♪
(八千代緑が丘校 轟)
=======================
一日体験の詳細・お申し込みはこちら!
https://www.jasmec.co.jp/toshin/event/taiken/
★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
<八千代緑が丘校 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
=======================