こんばんは。
八千代緑が丘校の轟です。
昨日のブログでは、三次関数の最大値・最小値問題
では、最大値・最小値の候補の大小を比較して
解を求めるやり方についてご紹介させて頂きました。
昨日挙げた具体例では、
最大値のみを求める問題でしたので、
場合分けをして解いたとしても、
それ程大きな手間ではありません。
ですから、
『慣れている、場合分けをする解法でよくない!?』
と思われた方もいらっしゃるかもしれません。

ただ、最大値と最小値の組み合わせを問われる
問題になると、事情が異なります。
場合分けの数が多くなるからです。
そのような具体的な問題はないかなぁ…と
記憶をたどってみると、そういえばッ!!
今春の同志社女子大学の入試問題で、
二次関数の最大値・最小値に関する問題が
出題されました。
その際、最大値M(a)、最小値m(a)と置いた際、
M(a) = 2m(a)を満たすaの値を問う問題が
出題されていました。

こういった問題で場合分けをしていると、
きっと途中で混乱してきてしまいそうだと
感じます。
ですから、作問者はきっと候補を挙げて、
そこから解を絞る解法で解くことを想定
しているのではないかと思うわけです。

最初に学校や塾で場合分けをする解法で習うと、
その解法から離れることに抵抗を感じる高校生も
いらっしゃるかもしれませんね。
ただ、問題の中には、最大値M(a)のグラフを描かせる
問題が出題されたりします。
ですから、その際に場合分けをしていると、
『わざわざ場合分けした後で、更に関数のグラフ描くんかいッ!
それって二度手間ではッ!?
どうせグラフを描くんでしょ!!』
とツッコミを入れたくなったり…。

ですから、
『とりあえず試しにやってみようかな』
ぐらいな感じで試してみて頂けたら幸いです。
(八千代緑が丘校の生徒たちには、
是非、この解法をマスターして頂きたいなと
願っています。)
さて、候補の中から絞る解法が役に立つなと
感じた問題をもう一つご紹介します。
今春の京都大学 文系の数学の入試問題です。
こちら↓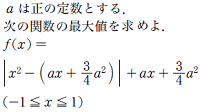
各予備校の解答を見ると、場合分けをした解法で
解いているのですが、さすが予備校の先生方、
手際良く解いた解答が掲載されています。
ただ、高校生がこんなに手際良くうまく場合分けをして
解くのは厳しいのではないかと、やはり思ってしまうんですね。
両方の解き方で解いてみて、その上で、
どちらの方が解きやすいのか、各自ご判断頂ければ
良いかなと思います。
それでは、今日も1日お疲れ様でした。
(八千代緑が丘校 轟)
=======================
10/27全国統一中学生テスト開催!詳細・お申込みはこちら!
https://www.jasmec.co.jp/toshin/event/zentochu/
11/4全国統一高校生テスト開催!詳細・お申込みはこちら!
https://www.jasmec.co.jp/toshin/event/zentoko/
一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/
<八千代緑が丘校 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
=======================