こんばんは。
八千代緑が丘校の轟です。
定期試験勉強に励む高2年生のAくんから
数学の質問を頂きました。

問題は、3次関数の最大値の問題でした。

学校や、多くの問題集では、
関数f(x)のグラフの形を考慮して
場合分けして求めると思います。
Aくんの使っている問題集にも、
場合分けする解法が掲載されておりました。
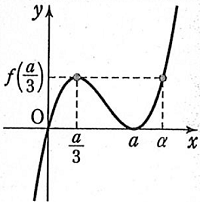
ただ、場合分けして求める解き方って
面倒ではありませんか?
最大値M(a)は、f(a/3) (ただし、a≦3) or f(1)の
どちらかのaの関数に絞られるわけですから、
このグラフを描いて、以下のように解を得る解法が
一番てっとり早いと思います。
0<a≦3/4のとき、f(1) ≧ f(a/3) ⇔ M(a) = f(1)
3/4<a≦3 のとき、f(a/3) ≧ f(1) ⇔ M(a) = f(a/3)
3≦a のとき、M(a) = f(1) 一択
(∵ f(a/3)の変域はa≦3のため)
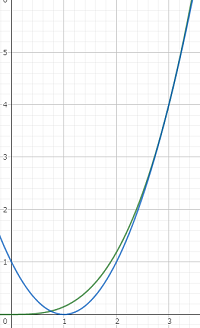
↑ 青い曲線:f(1)、緑の曲線:f(a/3)
特に入学試験のように制限時間があり、
点数によって合否が決まるような試験の場合は、
早く簡単に解く解法を選択した方がお薦めです。

ちなみに、このように最大値の候補を絞って、
候補同士の大小を比較する解き方は、
2次関数の最大値・最小値問題にも活用できます。
ですので、これまで場合分けして解いていた
という方は、一度今回ご紹介した解き方を
試してみてください。
(八千代緑が丘校 轟)
=======================
10/27全国統一中学生テスト開催!詳細・お申込みはこちら!
https://www.jasmec.co.jp/toshin/event/zentochu/
11/4全国統一高校生テスト開催!詳細・お申込みはこちら!
https://www.jasmec.co.jp/toshin/event/zentoko/
一日体験の詳細・お申し込みはこちら👇
https://www.jasmec.co.jp/toshin/event/taiken/
<八千代緑が丘校 校舎紹介ページ>
http://www.jasmec.co.jp/koushaguide/pym.htm
YouTubeはこちらから👇
https://youtu.be/KOoM-l4YrOE
★Instagramやってます★
フォローお願いします👇
https://www.instagram.com/honshin_premium/
=======================